凹凸函数的定义图像及性质，凹凸函数

1、在函数fx凹凸函数的图象上取任意两点凹凸函数，如果函数图象在这两点之间的部分总在连接这两点的线段的下方凹凸函数，那么这个函数就是凹函数同理可知，如果函数图像在这两点之间的部分总在连接这两点线段的上方，那么这个函数就是凸函数例子。

2、根据某函数的导数的导数，若其导数的导数大于0，即是凹函数，反之为凸。

3、函数凹凸性的判断方法是看导数，代数上，函数一阶导数为负，二阶导数为正或者一阶正，二阶负，便是凸的，一阶与二阶同号为凹函数在凹凸性发生改变的点称为拐点，拐点的二阶导数为0或不存在二阶导数1凹。

4、看导数，代数上，函数一阶导数为负，二阶导数为正或者一阶正，二阶负，便是凸的，一阶与二阶同号为凹函数在凹凸性发生改变的点称为拐点，拐点的二阶导数为0或不存在二阶导数函数凹凸性的定义 1凹函数定义设。

5、4用上述点将定义域分成若干小区间，看每个小区间上fx的二阶导的符号，来判断他的凹凸性大于零是凹函数，小于零是凸函数5若fx的二阶导在点x的两侧异号，则x，fx是拐点，否则不是。

6、凹凸两种判断方法1若fx在区间I上有一阶二阶导数，二阶导数fquotx0在区间I内为凹，反之为凸2函数fx在区间I上连续，如果对I上任意两点x1，x2恒有fx1+x22ltfx1+fx22则为凹。

7、讨论二阶导数的正负，若在某区间为正则为凹区间，若在某区间为负则为凸区间一般地，把满足fx1+fx22fx1+x22的区间称为函数fx的凹区间反之为凸区间凹凸性改变的点叫做拐点通常凹凸性由。

8、1已知函数表达式，但不容易做出图形是可以利用其二阶导数符号来判定函数的凹凸性 y#39#390是凹函数 y#39#39lt0是凸函数 2如果可以从函数的表达式入手做出其草图，也可从图形中判断其凹凸性，开口向下为凸，开口向上为凹3。

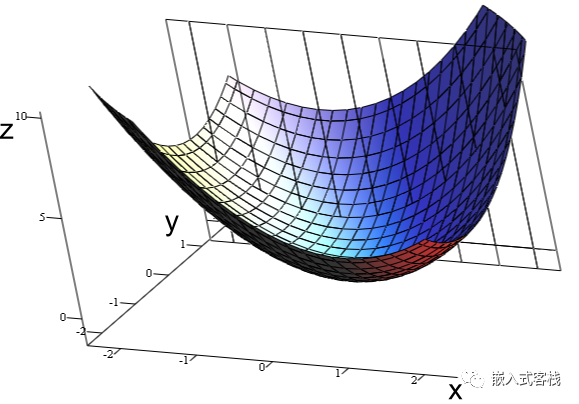
9、x1+x22，就是凹函数 对于对数函数，A表示fx1+x22，B表示 fx1+fx22，对任何函数就这样画，看A，B点高低即可 PSA点横坐标为x1+x22 大学里有根据二次求导来判断凹凸函数。

10、反例fx=1x是0，+oo上的凸函数，它的反函数显然不是凹函数 当然，你说的结论在一定的条件下还是可以修复的 开区间上的凸函数fx一定是连续函数，如果反函数存在就要求fx严格单调，当fx单调增时f^。

11、俺在新东方课件上学的，凹凸的定义以及几何意义如下设fx在区间I上连续，若对任意不同的亮点x1，x2，恒有fx1+x22fx1+fx22则称fx在I上是凸的，反之为凹在几何上，曲线y=fx上任意。

12、如果函数fx在区间I上二阶可导，则fx在区间I上是凹函数的充要条件是f#39#39x=0fx在区间I上是凸函数的充要条件是f#39#39xlt=012不过补充一下，中国数学界关于函数凹凸性定义和国外很多定义是反的。

13、凸函数的一阶导数是减函数，因此其二阶导数小于0凹函数的一阶导数是增函数，因此其二阶导数大于0当遇到需要知道二阶导数的正负时，图像的凹凸性就显得很重要比如运动函数s=ft，当只知道它的图像而不知道它的。

14、不过补充一下，中国数学界关于函数凹凸性定义和国外很多定义是反的Convex Function在国内的数学书中指凹函数Concave Function指凸函数在国内涉及经济学的很多书中，凹凸性的提法和国外的提法是一致的，也就是和单纯的。